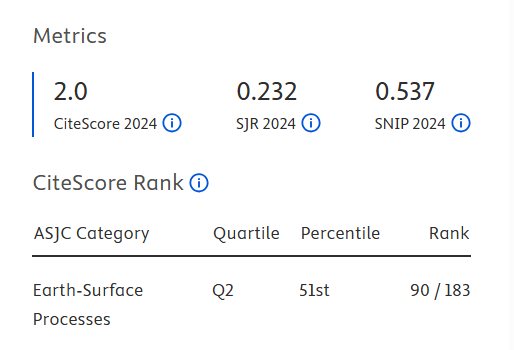
Classical Mechanics Theory and Schrödinger's Equation: A Derivation of Relations

Jiancao  Li; Yanchun Yu

doi:10.5614/j.eng.technol.sci.2025.57.5.1

Authors

Jiancao Li Chuzhou College, School of Civil and Architectural Engineering, Chuzhou 239000, China, China
Yanchun Yu
yanchunyu743@gmail.com
Northeast Agricultural University School of Water Conservancy and Architecture, Harbin 150000, China, China

Vol. 57 No. 5 (2025): Vol. 57 No. 5 (2025): October (In Progress)

Articles

Accepted July 28, 2025

Published September 23, 2025

Downloads

PDF

Abstract
How to Cite
Metrics
References
License

This study examines integrating the Schrödinger equation with classical mechanics using a virtual axis-to-dimensional expansion. One-dimensional material fluctuations are viewed in a two-dimensional plane, explaining the random nature of these fluctuations and their spatial and temporal trajectories. A quantum-consistent force field is proposed, with its strength determined by the Planck constant and inversely proportional to the distance from the stationary point. Newton's second law is applied to establish a second-order linear differential equation for material fluctuations, from which the standard one-dimensional Schrödinger equation is derived, showing their equivalence. The study extends the three-dimensional Schrödinger equation to include external forces and explains quantum phenomena like energy levels and transitions through particle trajectory changes. This approach connects classical mechanics and quantum mechanics, offering a concise and intuitive formulation with clear physical significance.

Li, J. ., & Yu, Y. (2025). Classical Mechanics Theory and Schrödinger’s Equation: A Derivation of Relations. Journal of Engineering and Technological Sciences, 57(5), 573–589. https://doi.org/10.5614/j.eng.technol.sci.2025.57.5.1

Download Citation

Andrianopoli, L., Cerchiai, B. L., Grassi, P. A., & Trigiante, M. (2019). The quantum theory of Chern-Simons supergravity. Journal of High Energy Physics, 2019(6), 1–22.

AS, B. G., Prasana, J. C., Muthu, S., Abraham, C. S., & David, H. A. (2019). Spectroscopic and quantum/classical mechanics based computational studies to compare the ability of andrographolide and its derivative to inhibit nitric oxide synthase. Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy, 218, 374–387.

Baiardi, A., Grimmel, S. A., Steiner, M., Türtscher, P. L., Unsleber, J. P., Weymuth, T., & Reiher, M. (2021). Expansive quantum mechanical exploration of chemical reaction paths. Accounts of Chemical Research, 55(1), 35–43.

Barrett, J., & Goldbring, I. (2023). A Nonstandard Formulation of Bohmian Mechanics.

Bass, S. D., & Doser, M. (2024). Quantum sensing for particle physics. Nature Reviews Physics, 1–11.

Boriev, I. A. (2018). Existence of dark matter with observed properties of cosmic microwave background radiation substantiates three conservation laws of classical physics and all principles of quantum mechanics as creates the value of Planck’s constant. Journal of Physics: Conference Series, 996(1), 012017.

Cerisola, F., Berritta, M., Scali, S., Horsley, S. A. R., Cresser, J. D., & Anders, J. (2024). Quantum–classical correspondence in spin–boson equilibrium states at arbitrary coupling. New Journal of Physics, 26(5), 053032.

Dai, M., & Yin, X. (2019). Unconditionally Optimal Error Estimates of the Semi-Implicit BDF2-FEM for Cubic Schrödinger Equations. Applied Mathematics and Mechanics, 40(6), 663–681. doi: 10.21656/1000-0887.390209

Feintzeig, B. H. (2022). The Classical–Quantum Correspondence. Cambridge University Press.

Finley, J. P. (2021). Developments of Bohmian Mechanics. ArXiv Preprint ArXiv:2110.01143.

Gudder, S., & Lahti, P. (2019). Paul Busch: at the heart of quantum mechanics. Foundations of Physics, 49(6), 457–459.

Kiukas, J., Lahti, P., Pellonpää, J.-P., & Ylinen, K. (2019). Complementary observables in quantum mechanics. Foundations of Physics, 49, 506–531.

Kramers, H. A. (2018). Quantum mechanics. Courier Dover Publications.

Li, C., Niu, M., Liu, P., Li, Y., & Wang, D. (2017). Combined multi-level quantum mechanics theories and molecular mechanics study of water-induced transition state of OH−+ CO2 reaction in aqueous solution. Chinese Physics B, 26(10), 103401.

Magri, L., Schmid, P. J., & Moeck, J. P. (2023). Linear flow analysis inspired by mathematical methods from quantum mechanics. Annual Review of Fluid Mechanics, 55(1), 541–574.

McIntyre, D. H. (2022). Quantum mechanics. Cambridge University Press.

Mills, R. L. (2003). Classical Quantum Mechanics. Physics Essays, 16(4).

Na, H. G., & Jin, C. (2019). Mass-energy equivalence in wave–particle duality of light: Integrated quantum and classical mechanics. Optik, 188, 71–77.

Pandir, Y., & Duzgun, H. H. (2019). New exact solutions of the space-time fractional cubic Schrodinger equation using the new type F-expansion method. Waves in Random and Complex Media, 29(3), 425–434.

Penati, S., & Polvara, D. (2019). Quantum anomalies in A r (1) Toda theories with defects. Journal of High Energy Physics, 2019(6), 1–39.

Rama, S. K. (2019). Non singular M theory universe in loop quantum cosmology—inspired models. General Relativity and Gravitation, 51(6), 75.

Rozema, L. A., Strömberg, T., Cao, H., Guo, Y., Liu, B.-H., & Walther, P. (2024). Experimental aspects of indefinite causal order in quantum mechanics. Nature Reviews Physics, 6(8), 483–499.

Schleich, W. P., Ranade, K. S., Anton, C., Arndt, M., Aspelmeyer, M., Bayer, M., Berg, G., Calarco, T., Fuchs, H., & Giacobino, E. (2016). Quantum technology: from research to application. Applied Physics B, 122, 1–31.

Shengfan, Z., Min, Z., & Huirong, T. A. N. (2019). Non-autonomous Schrödinger Lattice Equation. Acta Mathematicae Applicatae Sinica, 42(2), 145–161.

Shi, L.-F. & Nie, Z.W. (2017). Solutions to the Nonlinear Schrödinger Equation and Coupled Nonlinear Schrödinger Equations with a New G′/ (G+ G′)-Expansion Method. Applied Mathematics and Mechanics, 38(5), 539–552.

Song, Y., Zhao, S., Guo, F.-M., Yang, Y.-J., & Li, S.-Y. (2016). Electron excitation from ground state to first excited state: Bohmian mechanics method. Chinese Physics B, 25(3), 033204.

Troy, W. C. (2019). New singular standing wave solutions of the nonlinear Schrodinger equation. Journal of Differential Equations, 267(2), 979–1000.

Vijaywargia, B., & Lakshminarayan, A. (2025). Quantum-classical correspondence in quantum channels. Physical Review E, 111(1), 014210.

Yago Malo, J., Lepori, L., Gentini, L., & Chiofalo, M. L. (2024). Atomic Quantum Technologies for Quantum Matter and Fundamental Physics Applications. Technologies, 12(5), 64.

Zhao, H., Sun, C., Liu, X., Yin, H., & Shi, Y. (2019). Exploring the effect of aggregation-induced emission on the excited state intramolecular proton transfer for a bis-imine derivative by quantum mechanics and our own n-layered integrated molecular orbital and molecular mechanics calculations. Chinese Physics B, 28(1), 018201.